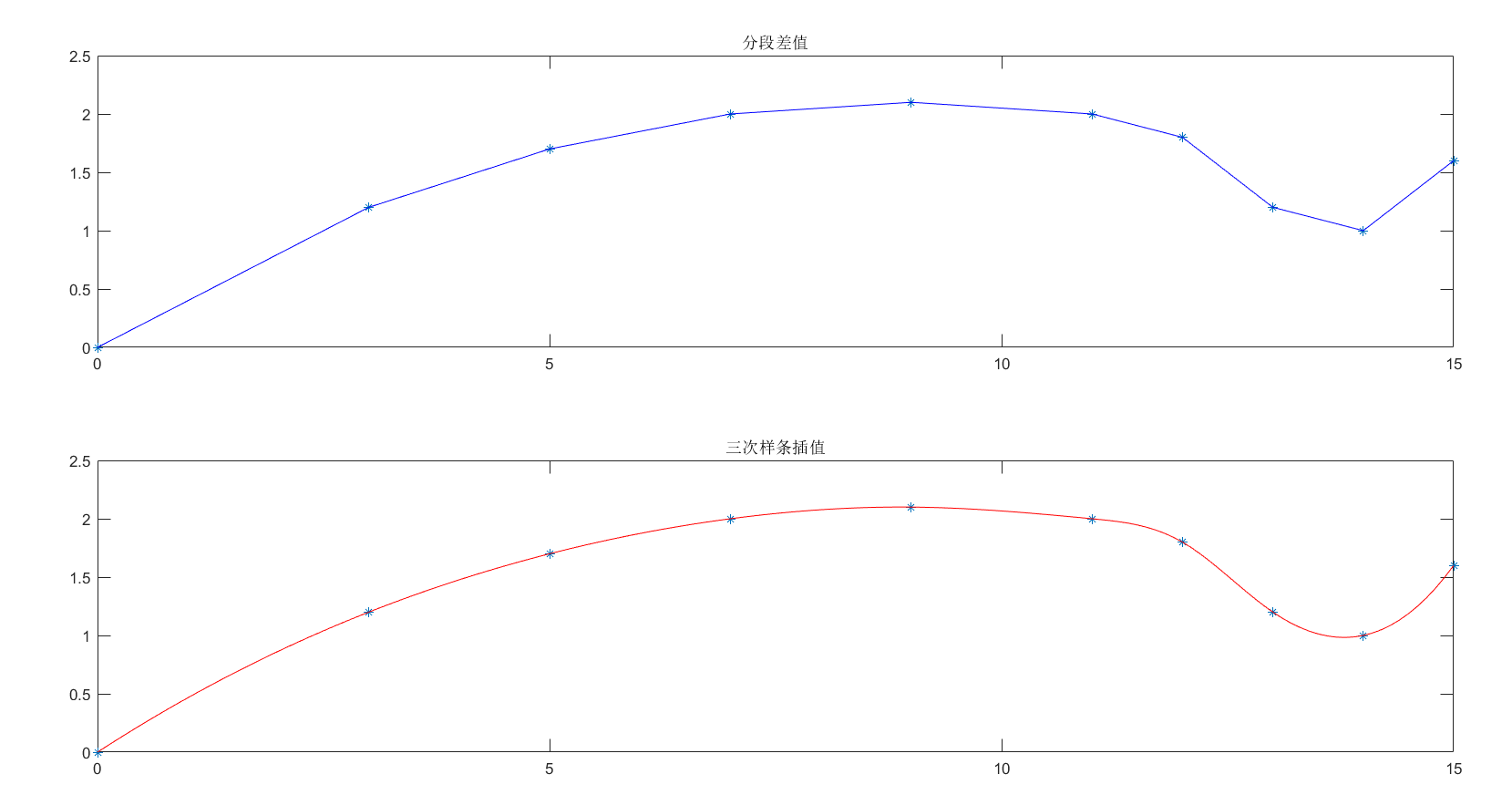
9.已知飞机下轮廓线上数据如下,分别用分段线性插值和三次样条插值求x每改变0.1时的y值。
x
0
3
5
7
9
11
12
13
14
15
y
0
1.2
1.7
2.0
2.1
2.0
1.8
1.2
1.0
1.6
1 2 3 4 5 6 7 8 9 10 11 12 13 x = [0 3 5 7 9 11 12 13 14 15 ]; y = [0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ]; xi = 0 :0.1 :15 ; y1 = interp1(x,y,xi,'linear' ); y2 = interp1(x,y,xi,'spline' ); subplot(2 ,1 ,1 ); plot (x,y,'*' ,xi,y1,'b' );title('分段差值' ) subplot(2 ,1 ,2 ); plot (x,y,'*' ,xi,y2,'r' );title('三次样条插值' )
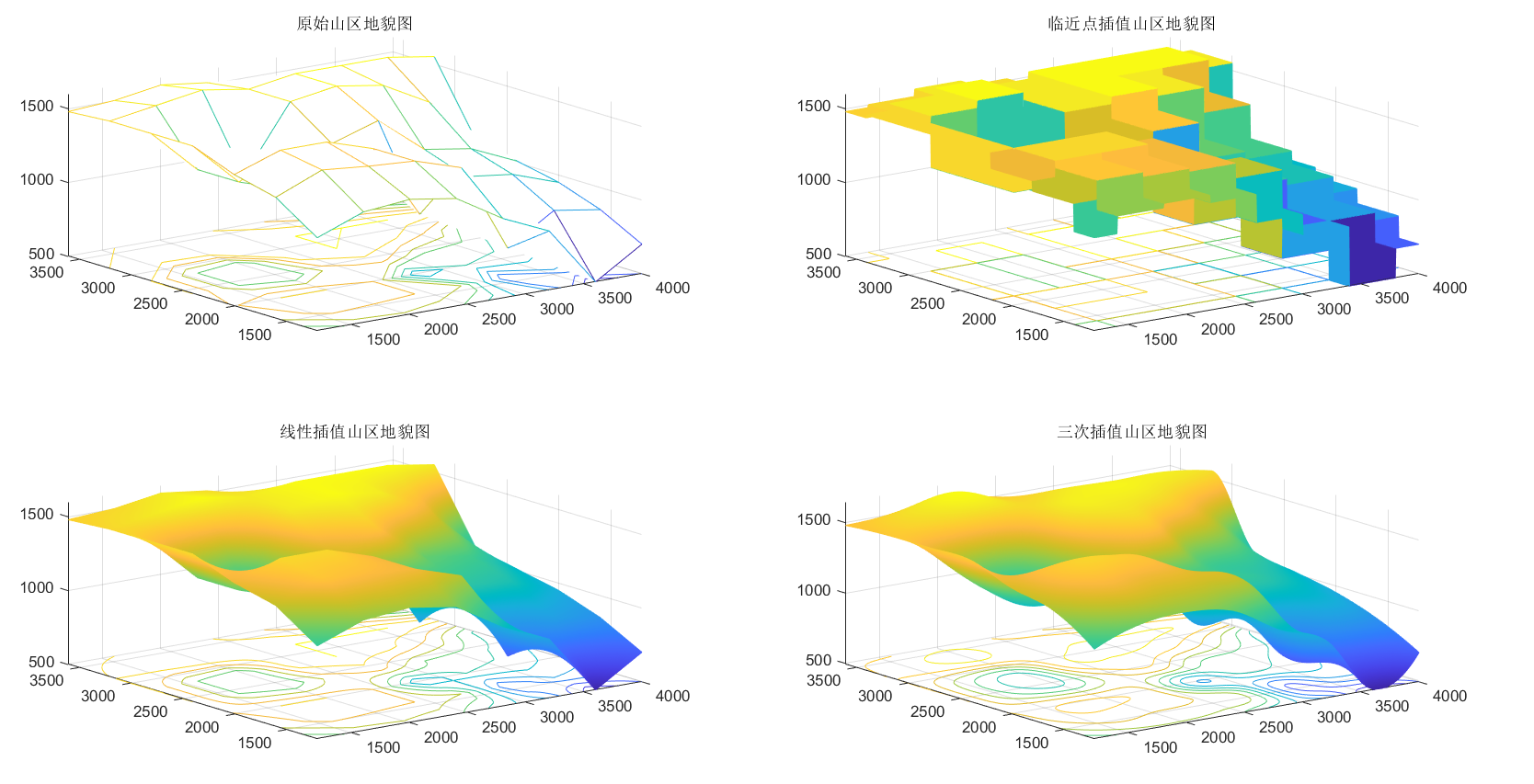
10.试作出该山区的地貌图和等高线图,并对最近邻点插值、双线性插值方法和双三次插值方法的插值效果进行比较。
1200
1600
2000
2400
2800
3200
3600
4000
1200
1130
1250
1280
1230
1040
900
500
700
1600
1320
1450
1420
1400
1300
700
900
850
2000
1390
1500
1500
1400
900
1100
1060
950
2400
1500
1200
1100
1350
1450
1200
1150
1010
2800
1500
1200
1100
1550
1600
1550
1380
1070
3200
1500
1550
1600
1550
1600
1600
1600
1550
3600
1480
1500
1550
1510
1430
1300
1200
980
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 clf; x=1200 :400 :4000 ; y=1200 :400 :3600 ; z=[1130 1250 1280 1230 1040 900 500 700 1320 1450 1420 1400 1300 700 900 850 1390 1500 1500 1400 900 1100 1060 950 1500 1200 1100 1350 1450 1200 1150 1010 1500 1200 1100 1550 1600 1550 1380 1070 1500 1550 1600 1550 1600 1600 1600 1550 1480 1500 1550 1510 1430 1300 1200 980 ]; subplot(2 ,2 ,1 ); meshc(x,y,z) title('原始山区地貌图' ); xi=1200 :5 :4000 ; yi=1200 :5 :3600 ; [xi,yi]=meshgrid (xi,yi); zi=interp2(x,y,z,xi,yi,'nearest' ); subplot(2 ,2 ,2 ); meshc(xi,yi,zi) title('临近点插值山区地貌图' ); zi=interp2(x,y,z,xi,yi,'linear' ); subplot(2 ,2 ,3 ); meshc(xi,yi,zi) title('线性插值山区地貌图' ); zi=interp2(x,y,z,xi,yi,'cubic' ); subplot(2 ,2 ,4 ); meshc(xi,yi,zi) title('三次插值山区地貌图' );
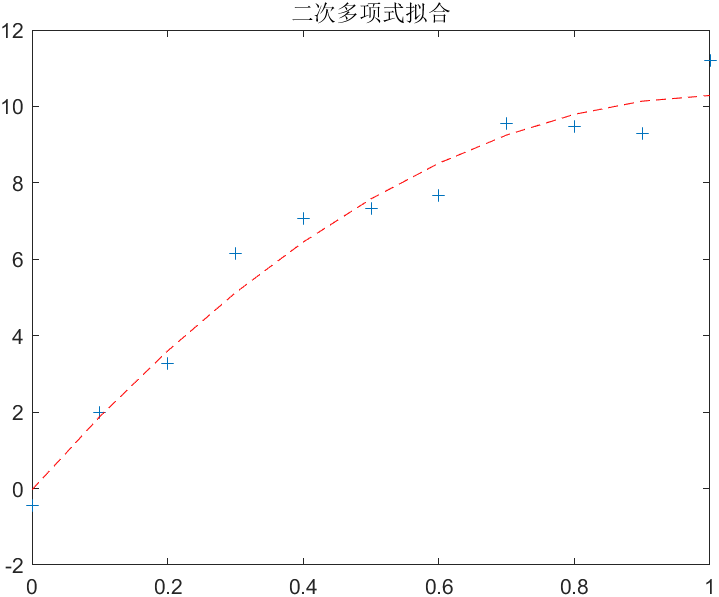
11.对下面一组数据作二次多项式拟合,并作出数据点和拟合曲线的图形
x
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
y
-0.447
1.978
3.28
6.16
7.08
7.34
7.66
9.56
9.48
9.30
11.2
1 2 3 4 5 6 7 8 x = 0 :0.1 :1 ; y = [-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2 ]; a =polyfit(x,y,2 ); z = polyval(a,x); clf; plot (x,y,'+' ,x,z,'--r' ) title('二次多项式拟合' );
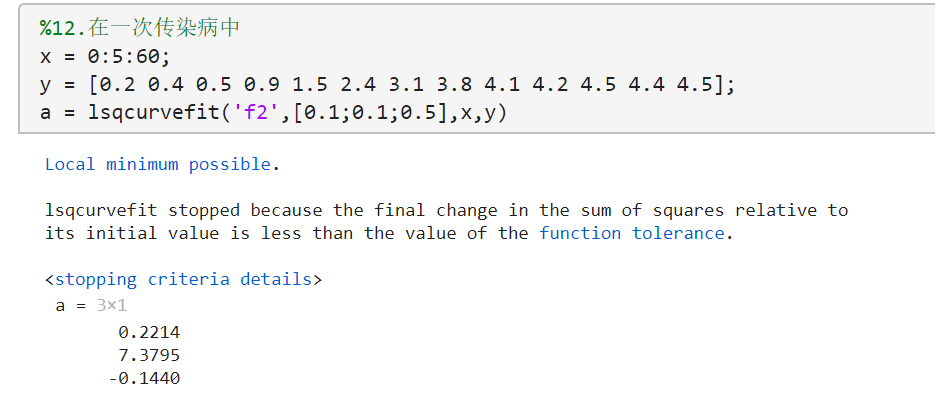
12.在一次传染病中,已知t时刻的染病人数I(t)满足模型I ( t ) = 1 a + b e c t I\left( t\right) =\dfrac{1}{a+be^{ct}} I ( t ) = a + b e c t 1
天数
0
5
10
15
20
25
30
35
40
45
50
55
60
感染人数
0.2
0.4
0.5
0.9
1.5
2.4
3.1
3.8
4.1
4.2
4.5
4.4
4.5
1 2 3 4 x = 0 :5 :60 ; y = [0.2 0.4 0.5 0.9 1.5 2.4 3.1 3.8 4.1 4.2 4.5 4.4 4.5 ]; a = lsqcurvefit('f2' ,[0.1 ;0.1 ;0.5 ],x,y)